Općinsko natjecanje 2002 SŠ1 1
Dodao/la:
arhiva2. travnja 2012. Neka su

,

i

međusobno različiti realni brojevi, od kojih nijedan nije jednak nuli, i za koje je
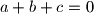
. Dokažite da vrijedi:
a)
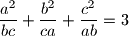
,
b)
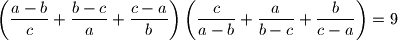
.
%V0
Neka su $a$, $b$ i $c$ međusobno različiti realni brojevi, od kojih nijedan nije jednak nuli, i za koje je $a+b+c=0$. Dokažite da vrijedi:
a) $\displaystyle{\frac{a^2}{bc}+\frac{b^2}{ca}+\frac{c^2}{ab}=3}$,
b) $\displaystyle{\left(\frac{a-b}{c}+\frac{b-c}{a}+
\frac{c-a}{b}\right)\left(\frac{c}{a-b}+\frac{a}{b-c}
+\frac{b}{c-a}\right)=9}$.
Izvor: Općinsko natjecanje iz matematike 2002