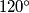
Dan je jednakokračan trokut kojemu je kut uz vrh jednak . Okomica iz tog vrha na krak trokuta dijeli trokut na dva trokuta od kojih tupokutan ima polumjer upisane kružnice . Kolika je površina trokuta ?
%V0
Dan je jednakokračan trokut $ABC$ kojemu je kut uz vrh $A$ jednak $120^\circ $. Okomica iz tog vrha na krak trokuta dijeli trokut na dva trokuta od kojih tupokutan ima polumjer upisane kružnice $1$. Kolika je površina trokuta $ABC$?
Školjka 
kojemu je kut uz vrh 
jednak 
. Okomica iz tog vrha na krak trokuta dijeli trokut na dva trokuta od kojih tupokutan ima polumjer upisane kružnice 
. Kolika je površina trokuta