Općinsko natjecanje 2003 SŠ1 4
Dodao/la:
arhiva2. travnja 2012. Ako za realne brojeve

,

,

vrijedi
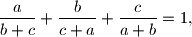
dokažite da je
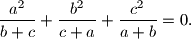
%V0
Ako za realne brojeve $a$, $b$, $c$ vrijedi $$\frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} = 1\text{,}$$ dokažite da je $$\frac{a^2}{b+c} + \frac{b^2}{c+a} + \frac{c^2}{a+b} = 0\text{.}$$
Izvor: Općinsko natjecanje iz matematike 2003