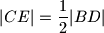
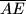
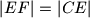
U pravokutnom trokutu točka je nožište visine iz vrha na hipotenuzu . Na kateti odabrana je točka tako da je , a na dužini točka tako da je . Dokažite da je .
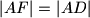
%V0
U pravokutnom trokutu $ABC$ točka $D$ je nožište visine iz vrha $C$ na hipotenuzu $\overline{AB}$. Na kateti $\overline{BC}$ odabrana je točka $E$ tako da je $\displaystyle{|CE|=\frac{1}{2}|BD|}$, a na dužini $\overline{AE}$ točka $F$ tako da je $|EF|=|CE|$. Dokažite da je $|AF|=|AD|$.
Školjka 
točka 
je nožište visine iz vrha 
na hipotenuzu 
. Na kateti 
odabrana je točka 
tako da je 
, a na dužini 
točka 
tako da je 
. Dokažite da je 
.