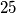
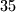
Nađi sve prirodne brojeve kojima je prva znamenka i koji zadovoljavaju uvjet da se uklanjanjem te prve znamenke dobije broj koji je puta manji od početnog. Dokaži da ne postoji prirodan broj sa svojstvom da se uklanjanjem njegove prve znamenke dobije broj koji je puta manji od .
%V0
$(a)$ Nađi sve prirodne brojeve kojima je prva znamenka $6$ i koji zadovoljavaju uvjet da se uklanjanjem te prve znamenke dobije broj koji je $25$ puta manji od početnog.
$(b)$ Dokaži da ne postoji prirodan broj $n$ sa svojstvom da se uklanjanjem njegove prve znamenke dobije broj koji je $35$ puta manji od $n$.
Školjka 
Nađi sve prirodne brojeve kojima je prva znamenka 
i koji zadovoljavaju uvjet da se uklanjanjem te prve znamenke dobije broj koji je 
puta manji od početnog.
Dokaži da ne postoji prirodan broj 
sa svojstvom da se uklanjanjem njegove prve znamenke dobije broj koji je 
puta manji od