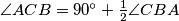
U trokutu vrijedi , a je polovište dužine . Kružnica sa središtem u točki siječe pravac u točkama i .
Dokaži da je .
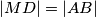
%V0
U trokutu $ABC$ vrijedi $\angle{ACB} = 90^{\circ} + \frac{1}{2} \angle{CBA}$, a $M$ je polovište dužine $\overline{BC}$. Kružnica sa središtem u točki $A$ siječe pravac $BC$ u točkama $M$ i $D$.
Dokaži da je $\left\vert MD \right\vert = \left\vert AB \right\vert$.
Školjka 
vrijedi 
, a 
je polovište dužine 
. Kružnica sa središtem u točki 
siječe pravac 
u točkama 
.
.