Državno natjecanje 2010 SŠ1 5
Kvaliteta:
Avg: 2,5Težina:
Avg: 3,3 Dana je dvadeset i jedna točka kao na slici.
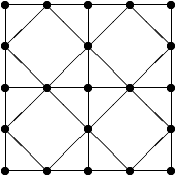
Na početku je svakoj točki pridružen broj nula. U svakom potezu odabire se pravac koji sadrži neku od nacrtanih dužina i u svim točkama kroz koje taj pravac prolazi, pridruženi brojevi se povećavaju za .
.
Kažemo da je prirodni broj dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj
dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj  .
.
a) Dokaži da je broj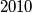 dohvatljiv.
dohvatljiv.
b) Dokaži da broj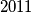 nije dohvatljiv.
nije dohvatljiv.

Na početku je svakoj točki pridružen broj nula. U svakom potezu odabire se pravac koji sadrži neku od nacrtanih dužina i u svim točkama kroz koje taj pravac prolazi, pridruženi brojevi se povećavaju za
 .
.Kažemo da je prirodni broj
 dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj
dohvatljiv ako se na opisani način može postići da je nakon određenog broja poteza svim točkama pridružen isti broj  .
.a) Dokaži da je broj
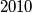 dohvatljiv.
dohvatljiv.b) Dokaži da broj
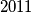 nije dohvatljiv.
nije dohvatljiv. Izvor: Državno natjecanje iz matematike 2010
 Školjka
Školjka 
