Općinsko natjecanje 1995 SŠ2 2
Dodao/la:
arhiva2. travnja 2012. Dokažite da jednadžba
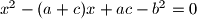
ima realne korijene
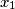
i
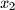
za bilo koje realne koeficijente

,

i

te da su

i

korijeni jednadžbe
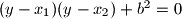
.
%V0
Dokažite da jednadžba $x^{2} - (a + c)x + ac - b^{2} = 0$ ima realne korijene $x_{1}$ i $x_{2}$ za bilo koje realne koeficijente $a$, $b$ i $c$ te da su $a$ i $c$ korijeni jednadžbe $(y - x_{1})(y - x_{2}) + b^{2} = 0$.
Izvor: Općinsko natjecanje iz matematike 1995