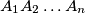
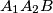
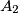
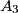
Izvan pravilnog mnogokuta nalazi se točka takva da je trokut jednakostraničan. Odredi sve za koje su točke , i uzastopni vrhovi nekog pravilnog mnogokuta.
%V0
Izvan pravilnog mnogokuta $A_1A_2 \ldots A_n$ nalazi se točka $B$ takva da je trokut $A_1A_2B$ jednakostraničan. Odredi sve $n$ za koje su točke $B$, $A_2$ i $A_3$ uzastopni vrhovi nekog pravilnog mnogokuta.
Školjka 
nalazi se točka 
takva da je trokut 
jednakostraničan. Odredi sve 
za koje su točke 
i 
uzastopni vrhovi nekog pravilnog mnogokuta.