Općinsko natjecanje iz matematike 2024, SŠ3 7
Komentari:
Ako prebacimo qˇ2 na drugu stranu, dobiti cemo razliku kvadrata. Očito je p > q, inaće bismo dobili da je r^n < 0, što ne može biti.
(p-q)(p+q) = r^n
primjetimo da ako su p i q neparni, da onda je njihova razlika i zbroj paran, te je onda r isto paran, odnosno r = 2
Ako je r=2, onda je p-q = 2ˇk i p+q = 2ˇm, pri čemu je 0 < k < m.
Iz ovoga slijedi da je (p+q)-(p-q) = 2^m-2^k => 2q = 2^k*(2^(m-k)-1) => q = 2^(k-1) * (2^(m-k)-1)
Ako je k > 1, onda je je q djeljiv s 2, pri čemu onda mora biti q=2. No kako su q i r parni, onda je i p paran pa je p=2, što je kontradikcija tvrdnji (ili možemo reći da je kontradikciji tvrdnji da je q paran i neparan u isto vrijeme). Stoga je k=1.
Ako je k=1, onda je q = 1* (2^(m-1)-1) = 2^(m-1)-1. Kako je m > k, tako je i m-k > 0 => m > 1.
Kako su p-q i p+q potencija broja 2, te kako smo odredili q pomoću m, možemo odrediti i p tako što znamo da je p=q+2^k => p=q+2 [razlika 2 prosta broja je 2^k, kako smo i definirali ali već znamo da je k=1 stoga možemo izračunati razlike].
Kako znamo p i q, možemo raspisati (p-q)(p+q) = 2*2^m = 2^(m+1), iz čega slijedi da je n = m+1.
Primjetimo da su p i q broj prije i broj nakon 2^x-tu, odnosno oni su +- 1 od tog broja. no kako su to 3 uzastopna broja, jedan od njih je djeljiv s 3, te kako to noje središnji, to mora biti q ili p. Jedini prosti broj dj. s 3 je 3, a to znači da imamo jedno rješenje za r = 2 => q = 3 i p = 5, iz čega slijedi n = 4.
Sada pretpostavimo da je r > 2. Iz razlike slijedi da je q = 2, odnosno (p-2)(p+2) = r^n. No opet ako p nije dj. s 3, onda je ili p-2 ili p+2 dj. s 3, te je r=3.
Za r=3 vidimo da je ili p-2 ili p+2 nedjeljiv s 3, te kako je p > q = 2, te je p nedjeljiv s 3, onda je p >= 5. No kako nijedan od p-2 ili p+2 nije jednak 0, očito ne može biti (p-2)(p+2) = 3^n.
Stoga je p=3, te dobivamo rješenje r = 5 i n = 1 za q = 2. I to su sva rješenja.
 Školjka
Školjka 

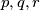 i prirodni broj
i prirodni broj  za koje vrijedi
za koje vrijedi 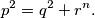 Nađi sva rješenja.
Nađi sva rješenja.