Općinsko natjecanje 1998 SŠ2 2
Dodao/la:
arhiva2. travnja 2012. Neka su
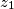
,
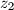
i
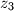
kompleksni brojevi za koje je
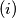
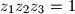
,
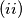
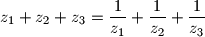
.
Dokažite da je barem jedan od njih jednak

.
%V0
Neka su $z_1$, $z_2$ i $z_3$ kompleksni brojevi za koje je
$(i)$ $z_1z_2z_3 = 1$,
$(ii)$ $z_1 + z_2 + z_3 = \dfrac{1}{z_1} + \dfrac{1}{z_2} + \dfrac{1}{z_3}$.
Dokažite da je barem jedan od njih jednak $1$.
Izvor: Općinsko natjecanje iz matematike 1998