Državno natjecanje 2011 SŠ1 3
Dodao/la:
arhiva1. travnja 2012. Četiri prirodna broja

,

,

,

zadovoljavaju jednakosti

Pokaži da postoji pravokutni trokut površine
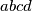
kojem su duljine svih stranica prirodni brojevi.
%V0
Četiri prirodna broja $a$, $b$, $c$, $d$ zadovoljavaju jednakosti $$ a+b=c \text{,} \qquad\qquad a+d=2c \text{.} $$ Pokaži da postoji pravokutni trokut površine $abcd$ kojem su duljine svih stranica prirodni brojevi.
Izvor: Državno natjecanje iz matematike 2011