Općinsko natjecanje 1999 SŠ2 3
Dodao/la:
arhiva2. travnja 2012. Neka je

trokut kod kojeg je
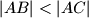
i neka je

polovište onog luka
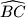
kružnice opisane tom trokutu na kojem leži točka

. Dokažite da za nožište

, okomice iz točke

na stranicu

, vrijedi jednakost
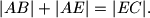
%V0
Neka je $ABC$ trokut kod kojeg je $|AB|<|AC|$ i neka je $D$ polovište onog luka $\widehat{BC}$ kružnice opisane tom trokutu na kojem leži točka $A$. Dokažite da za nožište $E$, okomice iz točke $D$ na stranicu $\overline{AC}$, vrijedi jednakost $$|AB|+|AE|=|EC|\text{.}$$
Izvor: Općinsko natjecanje iz matematike 1999