Općinsko natjecanje 2001 SŠ2 2
Dodao/la:
arhiva2. travnja 2012. Trokutu

sa stranicama duljina
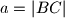
,
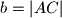
,
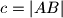
opisana je kružnica. Tangenta na tu kružnicu u točki

okomita je na stranicu

. Dokažite da je
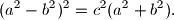
%V0
Trokutu $ABC$ sa stranicama duljina $a=|BC|$, $b=|AC|$, $c=|AB|$ opisana je kružnica. Tangenta na tu kružnicu u točki $C$ okomita je na stranicu $\overline{AB}$. Dokažite da je $$(a^2-b^2)^2 = c^2(a^2+b^2) \text{.}$$
Izvor: Općinsko natjecanje iz matematike 2001