Općinsko natjecanje 2006 SŠ2 1
Dodao/la:
arhiva2. travnja 2012. Odredi sve kompleksne brojeve

takve da vrijedi:

gdje su

i

(
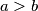
) rješenja kvadratne jednadžbe
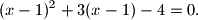
%V0
Odredi sve kompleksne brojeve $z$ takve da vrijedi: $$\mbox{Re}\,z=5 \cdot \mbox{Im}\,z \quad \text{i} \quad |z-(a+ib)|=5 \text{,}$$ gdje su $a$ i $b$ ($a>b$) rješenja kvadratne jednadžbe $$(x-1)^2+3(x-1)-4=0.$$
Izvor: Općinsko natjecanje iz matematike 2006