Općinsko natjecanje 2007 SŠ2 4
Dodao/la:
arhiva2. travnja 2012. Odredi sve realne parametre

za koje funkcija
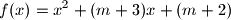
zadovoljava sljedeća dva uvjeta:

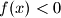
za sve
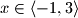
;

zbroj recipročnih vrijednosti nultočaka manji je od
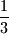
.
%V0
Odredi sve realne parametre $m$ za koje funkcija $$
f(x)=x^2+(m+3)x+(m+2)
$$ zadovoljava sljedeća dva uvjeta:
$a)$ $f(x)<0$ za sve $x\in \left< -1,3 \right>$;
$b)$ zbroj recipročnih vrijednosti nultočaka manji je od $\dfrac 13$.
Izvor: Općinsko natjecanje iz matematike 2007