Državno natjecanje 2012 SŠ1 4
Dodao/la:
arhiva1. travnja 2012. Neka je trokut

s tupim kutom kod vrha

, neka su

i

polovišta stranica

i

redom,

točka na stranici

takva da je
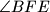
pravi, te

točka na dužini
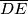
takva da je kut
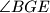
pravi.
Dokaži da točke

,

i

leže na istom pravcu ako i samo ako je
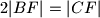
.
%V0
Neka je trokut $ABC$ s tupim kutom kod vrha $B$, neka su $D$ i $E$ polovišta stranica $\overline{AB}$ i $\overline{AC}$ redom, $F$ točka na stranici $\overline{BC}$ takva da je $\angle BFE$ pravi, te $G$ točka na dužini $\overline{DE}$ takva da je kut $\angle BGE$ pravi.
Dokaži da točke $A$, $F$ i $G$ leže na istom pravcu ako i samo ako je $2|BF|=|CF|$.
Izvor: Državno natjecanje iz matematike 2012