Lik
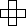
koji se sastoji od pet jediničnih kvadratića zovemo
plus. Na koliko se načina
plus može smjestiti na
ploču istog oblika koja se sastoji od
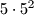
jediničnih kvadratića, tako da prekriva točno pet jediničnih kvadratića?
%V0
Lik $\setlength{\unitlength}{5pt}
\begin{picture}(3, 3)
\put(1, 0){\line(1, 0){1}}
\put(1, 0){\line(0, 1){3}}
\put(0, 1){\line(1, 0){3}}
\put(0, 1){\line(0, 1){1}}
\put(0, 2){\line(1, 0){3}}
\put(3, 1){\line(0, 1){1}}
\put(2, 0){\line(0, 1){3}}
\put(1, 3){\line(1, 0){1}}
\end{picture}$ koji se sastoji od pet jediničnih kvadratića zovemo [i]plus[/i]. Na koliko se načina [i]plus[/i] može smjestiti na [i]ploču[/i] istog oblika koja se sastoji od $5\cdot 5^2$ jediničnih kvadratića, tako da prekriva točno pet jediničnih kvadratića?