Općinsko natjecanje 1995 SŠ3 3
Dodao/la:
arhiva2. travnja 2012. Neka je

središte upisane kružnice trokuta

. Dokažite da vrijedi
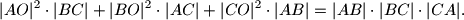
%V0
Neka je $O$ središte upisane kružnice trokuta $ABC$. Dokažite da vrijedi $$|AO|^{2}\cdot |BC| + |BO|^{2}\cdot |AC| + |CO|^{2}\cdot |AB| = |AB|\cdot |BC|\cdot |CA| \text{.}$$
Izvor: Općinsko natjecanje iz matematike 1995