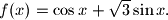
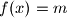
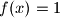
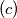
Odredite sve realne brojeve za koje jednadžba ima rješenje. Riješite jednadžbu . Nađite maksimum funkcije i odredite za koje vrijednosti se on postiže.
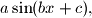
(Uputa: Prikažite funkciju u obliku gdje su , , .)
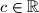
%V0
Zadana je funkcija $f(x)=\cos x+\sqrt{3}\sin x.$
$(a)$ Odredite sve realne brojeve $m$ za koje jednadžba $f(x)=m$ ima rješenje.
$(b)$ Riješite jednadžbu $f(x)=1$.
$(c)$ Nađite maksimum funkcije $f(x)$ i odredite za koje vrijednosti $x$ se on postiže.
([i]Uputa:[/i] Prikažite funkciju $f(x)$ u obliku $a\sin (bx+c),$ gdje su $a$, $b$, $c \in \mathbb{R}$.)
Školjka 
Odredite sve realne brojeve 
za koje jednadžba 
ima rješenje.
Riješite jednadžbu 
.
Nađite maksimum funkcije 
i odredite za koje vrijednosti 
se on postiže.
gdje su 
, 
, 
.)