Školjka

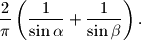
%V0 Oko kružnice polumjera $r$ opisan je trapez kojemu su kutovi uz dulju osnovicu $\alpha$ i $\beta$. Dokažite da je omjer površina trapeza i kruga jednak $$\dfrac{2}{\pi } \left( \dfrac{1}{\sin \alpha }+\dfrac{1}{\sin \beta } \right) \text{.}$$