Općinsko natjecanje 2000 SŠ3 4
Dodao/la:
arhiva2. travnja 2012. Dana je funkcija
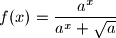
, gdje je

pozitivan realan broj. Odredite
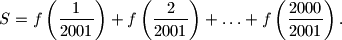
%V0
Dana je funkcija $f(x)=\displaystyle{\frac{a^x}{a^x+\sqrt{a}}}$, gdje je $a$ pozitivan realan broj. Odredite $$
S=f\left(\frac{1}{2001}\right)+f\left(\frac{2}{2001}\right)+ \ldots +
f\left(\frac{2000}{2001}\right).
$$
Izvor: Općinsko natjecanje iz matematike 2000