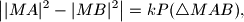
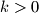
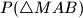
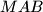
U ravnini su dane dvije različite točke i . Dokažite da se skup točaka , takvih da je gdje je dana konstanta i površina trokuta , sastoji od dva pravca.
%V0
U ravnini su dane dvije različite točke $A$ i $B$. Dokažite da se skup točaka $M$, takvih da je $$
\left||MA|^2-|MB|^2\right|=kP(\triangle MAB),
$$ gdje je $k>0$ dana konstanta i $P(\triangle MAB)$ površina trokuta $MAB$, sastoji od dva pravca.
Školjka 
i 
. Dokažite da se skup točaka 
, takvih da je 
gdje je 
dana konstanta i 
površina trokuta 
, sastoji od dva pravca.