Što je Školjka?
Školjka je web arhiva zadataka iz matematike, pomoćni alat i sredstvo motivacije namijenjen učenicima i studentima pri pripremi za natjecanja. Sadrži tisuće i tisuće zadataka s raznih matematičkih natjecanja u prethodnih dvadesetak godina te se redovito nadopunjava novim zadacima i natjecanjima.
Why Školjka?
Osim što služi kao baza zadataka, Školjka omogućuje pretraživanje istih po kategorijama i po težini. Učenici tako mogu jednostavno pronaći zadatke točno onog tipa koji ih zanima. Također, Školjka može biti od velike pomoći njihovim mentorima pri organizaciji priprema i predavanja.
Odabrana natjecanja
Nedavno objavljeni zadaci
Odredi sve prirodne brojeve  za koje je vrijednost izraza
za koje je vrijednost izraza 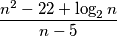 cijeli broj.
cijeli broj.
Odredi sve prirodne brojeve $n$ za koje je vrijednost izraza
\[
\frac{n^2 - 22 + \log_2 n }{n-5}
\]
cijeli broj.
1 godina, 3 mjeseci
Odredi sve trojke prirodnih brojeva $(m,n,k)$ za koje vrijedi
\[ D(m,20)=n, \quad D(n,15)=k \quad \text{i} \quad D(m,k)=5,\]
pri čemu je $D(a,b)$ najveći zajednički djelitelj brojeva $a$ i $b$.
1 godina, 3 mjeseci
Nedavne aktivnosti:
24. siječnja
00:53
Osoba je označio/la kao riješen zadatak
23. siječnja
22:23
roko937 je označio/la s To Do zadatak
22:21
roko937 je označio/la s To Do zadatak
21:57
roko937 je označio/la s To Do zadatak
21:52
msaric je označio kao riješen zadatak
21:48
msaric je označio kao riješen zadatak
21:26
roko937 je označio/la s To Do zadatak
21:16
roko937 je označio/la kao riješen zadatak
21:07
roko937 je označio/la kao riješen zadatak
21:01
roko937 je označio/la kao riješen zadatak
20:58
roko937 je označio/la kao riješen zadatak
20:45
roko937 je označio/la kao riješen zadatak
20:11
roko937 je označio/la kao riješen zadatak
20:03
roko937 je označio/la kao riješen zadatak
19:01
msaric je označio kao riješen zadatak
18:52
msaric je označio kao riješen zadatak
18:35
msaric je označio kao riješen zadatak
18:35
msaric je označio kao riješen zadatak
14:05
roko937 je označio/la kao riješen zadatak
22. siječnja
23:49
roko937 je označio/la kao riješen zadatak
23:30
roko937 je označio/la kao riješen zadatak
23:12
roko937 je označio/la kao riješen zadatak
22:49
roko937 je označio/la s To Do zadatak
22:45
roko937 je označio/la kao riješen zadatak
22:24
roko937 je označio/la s To Do zadatak
21:44
roko937 je označio/la kao riješen zadatak
21:39
roko937 je označio/la kao riješen zadatak
21:26
roko937 je označio/la kao riješen zadatak
21:06
roko937 je označio/la kao riješen zadatak
20:57
roko937 je označio/la s To Do zadatak
 Školjka
Školjka  za koje je vrijednost izraza
za koje je vrijednost izraza 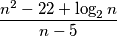 cijeli broj.
cijeli broj. 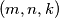 za koje vrijedi
za koje vrijedi 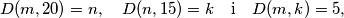 pri čemu je
pri čemu je 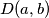 najveći zajednički djelitelj brojeva
najveći zajednički djelitelj brojeva  i
i  .
.