Let  be a positive integer. Consider words of length
be a positive integer. Consider words of length  composed of letters from the set
composed of letters from the set 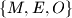 . Let
. Let  be the number of such words containing an even number (possibly 0) of blocks
be the number of such words containing an even number (possibly 0) of blocks 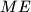 and an even number (possibly 0) blocks of
and an even number (possibly 0) blocks of 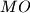 . Similarly let
. Similarly let  the number of such words containing an odd number of blocks
the number of such words containing an odd number of blocks 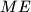 and an odd number of blocks
and an odd number of blocks 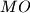 . Prove that
. Prove that 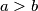 .
.
 be a positive integer. Consider words of length
be a positive integer. Consider words of length  composed of letters from the set
composed of letters from the set 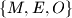 . Let
. Let  be the number of such words containing an even number (possibly 0) of blocks
be the number of such words containing an even number (possibly 0) of blocks 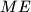 and an even number (possibly 0) blocks of
and an even number (possibly 0) blocks of 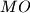 . Similarly let
. Similarly let  the number of such words containing an odd number of blocks
the number of such words containing an odd number of blocks 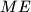 and an odd number of blocks
and an odd number of blocks 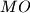 . Prove that
. Prove that 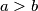 .
. Let  be a convex quadrilateral with no pair of parallel sides, such that
be a convex quadrilateral with no pair of parallel sides, such that 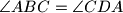 . Assume that the intersections of the pairs of neighbouring angle bisectors of
. Assume that the intersections of the pairs of neighbouring angle bisectors of  form a convex quadrilateral
form a convex quadrilateral 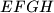 . Let
. Let  be the intersection of the diagonals of
be the intersection of the diagonals of 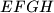 . Prove that the lines
. Prove that the lines  and
and  intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle 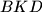 .
.
 be a convex quadrilateral with no pair of parallel sides, such that
be a convex quadrilateral with no pair of parallel sides, such that 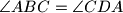 . Assume that the intersections of the pairs of neighbouring angle bisectors of
. Assume that the intersections of the pairs of neighbouring angle bisectors of  form a convex quadrilateral
form a convex quadrilateral 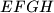 . Let
. Let  be the intersection of the diagonals of
be the intersection of the diagonals of 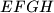 . Prove that the lines
. Prove that the lines  and
and  intersect on the circumcircle of the triangle
intersect on the circumcircle of the triangle 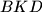 .
.  Školjka
Školjka 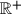 denote the set of all positive real numbers. Find all functions
denote the set of all positive real numbers. Find all functions 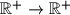 such that
such that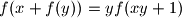
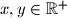 .
.  be a positive integer. A set
be a positive integer. A set 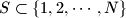 is called allowed if it does not contain three distinct elements
is called allowed if it does not contain three distinct elements 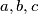 such that
such that  . Determine the largest possible number of elements in an allowed set
. Determine the largest possible number of elements in an allowed set  .
. 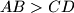 , the line
, the line  bisects the angle
bisects the angle 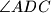 . The line through
. The line through  parallel to
parallel to  meets the segments
meets the segments  and
and  , respectively. Let
, respectively. Let  be the circumcenter of the triangle
be the circumcenter of the triangle 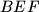 . Suppose that
. Suppose that 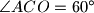 . Prove the equality
. Prove the equality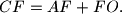
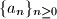 is defined by
is defined by 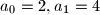 and
and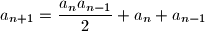
 for which there exists a positive integer
for which there exists a positive integer  such that
such that 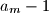 .
. 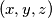 of real numbers such that
of real numbers such that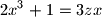
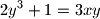
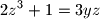
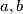 and
and 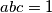 . Prove that
. Prove that 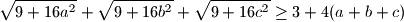
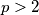 be a prime number. For any permutation
be a prime number. For any permutation 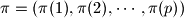 of the set
of the set 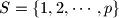 , let
, let 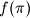 denote the number of multiples of
denote the number of multiples of 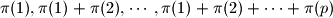
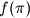 taken over all permutations
taken over all permutations 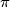 of
of  . Let
. Let  and
and  be points on the sides
be points on the sides  and
and  , respectively, such that
, respectively, such that 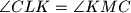 . Prove that the perpendiculars to the sides
. Prove that the perpendiculars to the sides 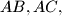 and
and 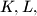 and
and 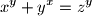
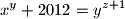
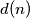 denote the number of positive divisors of
denote the number of positive divisors of 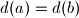 and
and 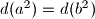 , but
, but 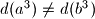 ?
?