All positive divisors of a positive integer  are written on a blackboard. Two players
are written on a blackboard. Two players  and
and  play the following game taking alternate moves. In the firt move, the player
play the following game taking alternate moves. In the firt move, the player  erases
erases  . If the last erased number is
. If the last erased number is  , then the next player erases either a divisor of
, then the next player erases either a divisor of  or a multiple of
or a multiple of  . The player who cannot make a move loses. Determine all numbers
. The player who cannot make a move loses. Determine all numbers  for which
for which  can win independently of the moves of
can win independently of the moves of  .
.
 are written on a blackboard. Two players
are written on a blackboard. Two players  and
and  play the following game taking alternate moves. In the firt move, the player
play the following game taking alternate moves. In the firt move, the player  erases
erases  . If the last erased number is
. If the last erased number is  , then the next player erases either a divisor of
, then the next player erases either a divisor of  or a multiple of
or a multiple of  . The player who cannot make a move loses. Determine all numbers
. The player who cannot make a move loses. Determine all numbers  for which
for which  can win independently of the moves of
can win independently of the moves of  .
. In each vertex of a regular  -gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let
-gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let 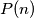 be the number of possible results of the shooting. Prove that for every positive integer
be the number of possible results of the shooting. Prove that for every positive integer 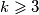 ,
, 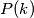 and
and 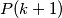 are relatively prime.
are relatively prime.
 -gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let
-gon, there is a fortress. At the same moment, each fortress shoots one of the two nearest fortresses and hits it. The result of the shooting is the set of the hit fortresses; we do not distinguish whether a fortress was hit once or twice. Let 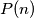 be the number of possible results of the shooting. Prove that for every positive integer
be the number of possible results of the shooting. Prove that for every positive integer 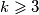 ,
, 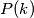 and
and 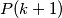 are relatively prime.
are relatively prime. Let  be a positive integer. A square
be a positive integer. A square  is partitioned into
is partitioned into 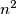 unit squares. Each of them is divided into two triangles by the diagonal parallel to
unit squares. Each of them is divided into two triangles by the diagonal parallel to  . Some of the vertices of the unit squares are colored red in such a way that each of these
. Some of the vertices of the unit squares are colored red in such a way that each of these 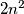 triangles contains at least one red vertex. Find the least number of red vertices.
triangles contains at least one red vertex. Find the least number of red vertices.
 be a positive integer. A square
be a positive integer. A square  is partitioned into
is partitioned into 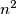 unit squares. Each of them is divided into two triangles by the diagonal parallel to
unit squares. Each of them is divided into two triangles by the diagonal parallel to  . Some of the vertices of the unit squares are colored red in such a way that each of these
. Some of the vertices of the unit squares are colored red in such a way that each of these 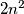 triangles contains at least one red vertex. Find the least number of red vertices.
triangles contains at least one red vertex. Find the least number of red vertices.  Školjka
Školjka 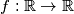 such that for all
such that for all 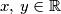 , we have
, we have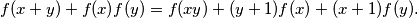
 on the diagonal
on the diagonal  such that
such that 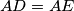 and
and 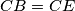 . Let
. Let  be the center of the circumcircle
be the center of the circumcircle  of the triangle
of the triangle 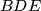 . The circle
. The circle  . Prove that the lines
. Prove that the lines 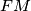 ,
,  and
and  meet at one point.
meet at one point.  and
and  of
of 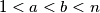 , the number
, the number 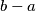 divides
divides 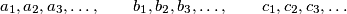
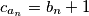 ;
;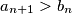 ;
;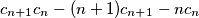 is even.
is even.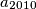 ,
, 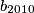 and
and 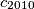 .
. 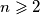 , determine the largest real constant
, determine the largest real constant 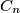 such that for all positive real numbers
such that for all positive real numbers 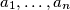 we have
we have 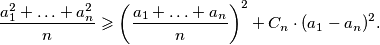
 touches the sides
touches the sides  , and
, and  in the points
in the points  ,
,  be the point symmetric to
be the point symmetric to 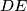 and
and 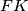 intersect at
intersect at  . Prove that
. Prove that 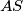 is parallel to
is parallel to  ,
, 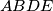 is a parallelogram. The diagonals
is a parallelogram. The diagonals 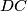 intersect at
intersect at 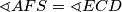 .
.  to be the positive integer with decimal representation
to be the positive integer with decimal representation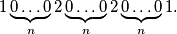
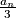 is always the sum of two positive perfect cubes but never the sum of two perfect squares.
is always the sum of two positive perfect cubes but never the sum of two perfect squares.  with the following two properties:
with the following two properties: