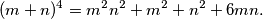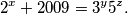Suppose that we have 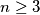 distinct colours. Let
distinct colours. Let  be the greatest integer with the property that every side and every diagonal of a convex polygon with
be the greatest integer with the property that every side and every diagonal of a convex polygon with  vertices can be coloured with one of
vertices can be coloured with one of  colours in the following way:
colours in the following way:
(i) At least two colours are used,
(ii) any three vertices of the polygon determine either three segments of the same colour or of three different colours.
Show that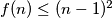 with equality for infintely many values of
with equality for infintely many values of  .
.
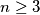 distinct colours. Let
distinct colours. Let  be the greatest integer with the property that every side and every diagonal of a convex polygon with
be the greatest integer with the property that every side and every diagonal of a convex polygon with  vertices can be coloured with one of
vertices can be coloured with one of  colours in the following way:
colours in the following way: (i) At least two colours are used,
(ii) any three vertices of the polygon determine either three segments of the same colour or of three different colours.
Show that
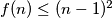 with equality for infintely many values of
with equality for infintely many values of  .
. The numbers  ,
,  ,
,  ,
,  (
(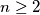 ) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let
) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let 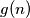 be the smallest possible number of integers left on the blackboard at the end. Find
be the smallest possible number of integers left on the blackboard at the end. Find 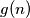 for every
for every  .
.
 ,
,  ,
,  ,
,  (
(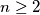 ) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let
) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let 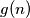 be the smallest possible number of integers left on the blackboard at the end. Find
be the smallest possible number of integers left on the blackboard at the end. Find 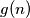 for every
for every  .
. We colour every square of the 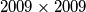 board with one of
board with one of  colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum
colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum  , such that for every colouring of the board at least on colour present at the board is connected.
, such that for every colouring of the board at least on colour present at the board is connected.
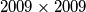 board with one of
board with one of  colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum
colours (we do not have to use every colour). A colour is called connected if either there is only one square of that colour or any two squares of the colour can be reached from one another by a sequence of moves of a chess queen without intermediate stops at squares having another colour (a chess quen moves horizontally, vertically or diagonally). Find the maximum  , such that for every colouring of the board at least on colour present at the board is connected.
, such that for every colouring of the board at least on colour present at the board is connected.  Školjka
Školjka  , such that
, such that 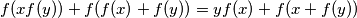 holds for all
holds for all  ,
, 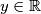 , where
, where 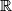 denotes the set of real numbers.
denotes the set of real numbers.  be a convex quadrilateral such that
be a convex quadrilateral such that  and
and  are not parallel and
are not parallel and 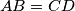 . The midpoints of the diagonals
. The midpoints of the diagonals  and
and  are
are  and
and  , respectively. The line
, respectively. The line  meets segments
meets segments  and
and  , respectively. Show that
, respectively. Show that 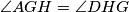 .
. 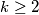 such that for all pairs
such that for all pairs 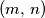 of different positive integers not greater than
of different positive integers not greater than  , the number
, the number 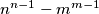 is not divisible by
is not divisible by  ,
,  be real numbers satisfying
be real numbers satisfying 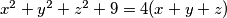 . Prove that
. Prove that 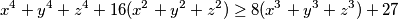 and determine when equality holds.
and determine when equality holds.  ,
,  ,
,  be real numbers such that for every two of the equations
be real numbers such that for every two of the equations 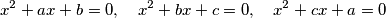 there is exactly one real number satisfying both of them. Determine all possible values of
there is exactly one real number satisfying both of them. Determine all possible values of 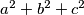 .
. 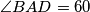 and denote by
and denote by 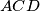 meets the line
meets the line 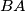 at
at 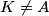 , the line
, the line 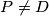 and the line
and the line  at
at 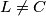 . The line
. The line 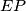 intersects the circumcircle of triangle
intersects the circumcircle of triangle 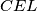 at points
at points  . Prove that triangles
. Prove that triangles 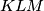 and
and 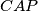 are congruent.
are congruent. 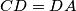 . Points
. Points 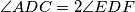 . Segments
. Segments 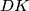 and
and 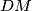 are height and median of triangle
are height and median of triangle 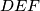 , respectively.
, respectively.  is the point symmetric to
is the point symmetric to  with respect to
with respect to 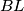 are parallel.
are parallel.