Consider a 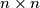 checkerboard with
checkerboard with 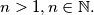 How many possibilities are there to put
How many possibilities are there to put 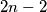 identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the
identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the 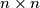 square.
square.
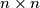 checkerboard with
checkerboard with 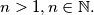 How many possibilities are there to put
How many possibilities are there to put 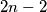 identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the
identical pebbles on the checkerboard (each on a different field/place) such that no two pebbles are on the same checkerboard diagonal. Two pebbles are on the same checkerboard diagonal if the connection segment of the midpoints of the respective fields are parallel to one of the diagonals of the 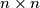 square.
square.  Školjka
Školjka 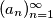 be a sequence of integers with
be a sequence of integers with 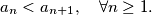 For all quadruple
For all quadruple 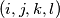 of indices such that
of indices such that 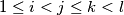 and
and 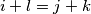 we have the inequality
we have the inequality 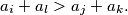 Determine the least possible value of
Determine the least possible value of 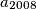 .
.  be an isosceles triangle with
be an isosceles triangle with 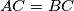 . Its incircle touches
. Its incircle touches  in
in  and
and  in
in  . A line distinct of
. A line distinct of 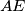 goes through
goes through  and intersects the incircle in
and intersects the incircle in  and
and  . Line
. Line  and
and 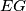 in
in  and
and  , respectively. Prove that
, respectively. Prove that 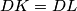 .
. 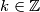 such that
such that 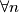 the numbers
the numbers 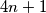 and
and 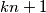 have no common divisor.
have no common divisor. 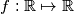 such that
such that 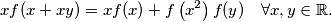
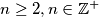 numbers. In each step we select two numbers from the blackboard and replace both of them by their sum. Determine all numbers
numbers. In each step we select two numbers from the blackboard and replace both of them by their sum. Determine all numbers  for which it is possible to yield
for which it is possible to yield  are on distinct sides of the line
are on distinct sides of the line  , and
, and 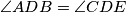 ,
, 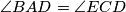 , and
, and 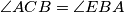 . Prove that
. Prove that  and
and 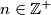 is a power of two, then the number/amount of the divisors is a power of two.
is a power of two, then the number/amount of the divisors is a power of two.