Prvo kolo
Za sustav novčanica 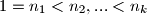 kažemo da je dobar ako "greedy" postupak vraćanja novca uvijek rezultira s najmanjim brojem isplaćenih novčanica. Dokažite da je sustav
kažemo da je dobar ako "greedy" postupak vraćanja novca uvijek rezultira s najmanjim brojem isplaćenih novčanica. Dokažite da je sustav 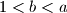 dobar ako i samo ako postoji
dobar ako i samo ako postoji  takav da je
takav da je 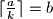 .
.
Napomena: U greedy postupku u svakom koraku vraćamo najviše moguće najvećih mogućih novčanica. Nadalje, označava najmanji cijeli broj veći od (ili jednak)
označava najmanji cijeli broj veći od (ili jednak)  .
.
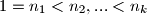 kažemo da je dobar ako "greedy" postupak vraćanja novca uvijek rezultira s najmanjim brojem isplaćenih novčanica. Dokažite da je sustav
kažemo da je dobar ako "greedy" postupak vraćanja novca uvijek rezultira s najmanjim brojem isplaćenih novčanica. Dokažite da je sustav 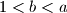 dobar ako i samo ako postoji
dobar ako i samo ako postoji  takav da je
takav da je 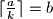 .
.Napomena: U greedy postupku u svakom koraku vraćamo najviše moguće najvećih mogućih novčanica. Nadalje,
 označava najmanji cijeli broj veći od (ili jednak)
označava najmanji cijeli broj veći od (ili jednak)  .
.  Školjka
Školjka  ,
,  i
i  pozitivni realni brojevi takvi da je
pozitivni realni brojevi takvi da je 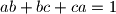 . Pokažite da vrijedi
. Pokažite da vrijedi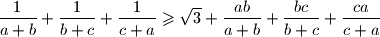
 je moguće postaviti konačan broj kraljica na beskonačnu šahovsku ploču tako da svaka napada točno
je moguće postaviti konačan broj kraljica na beskonačnu šahovsku ploču tako da svaka napada točno  u pravokutniku
u pravokutniku  odabrana je tako da je
odabrana je tako da je 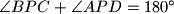 . Odredi sumu kutova
. Odredi sumu kutova 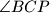 i
i 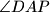 .
. 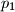 ,
, 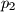 ,
,  ,
, 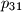 . Dokaži da, ako
. Dokaži da, ako  dijeli sumu njihovih četvrtih potencija, među njima postoje
dijeli sumu njihovih četvrtih potencija, među njima postoje  uzastopna prosta.
uzastopna prosta. 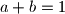 ,
, 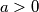 ,
, 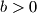 . Dokažite da je
. Dokažite da je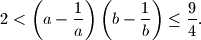
 sastoji se od
sastoji se od 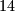 prirodnih brojeva. Pokažite da postoji
prirodnih brojeva. Pokažite da postoji 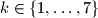 za koji je moguće naci
za koji je moguće naci  i
i  skupa
skupa 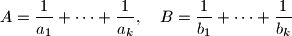 razlikuju za manje od
razlikuju za manje od 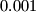 .
. 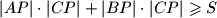 .
.  za koje vrijedi
za koje vrijedi 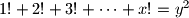 .
. 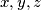 za koje istovremeno vrijedi
za koje istovremeno vrijedi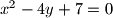 ,
, 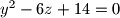 i
i 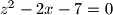 .
. 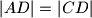 i
i 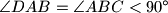 . Pravac kroz
. Pravac kroz  i polovište
i polovište  siječe pravac
siječe pravac  u točki
u točki  . Dokažite da je
. Dokažite da je 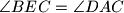 .
.  postoji
postoji 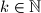 takav da
takav da 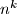 ima istu prvu i zadnju znamenku u bazi
ima istu prvu i zadnju znamenku u bazi  ?
?