Juniorska balkanska matematička olimpijada
[ JBMO ]
Let  be a positive integer. Two players, Alice and Bob, are playing the following game:
be a positive integer. Two players, Alice and Bob, are playing the following game:
- Alice chooses n real numbers; not necessarily distinct.
- Alice writes all pairwise sums on a sheet of paper and gives it to Bob. (There are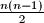 such sums; not necessarily distinct.)
such sums; not necessarily distinct.)
- Bob wins if he finds correctly the initial n numbers chosen by Alice with only one guess.
Can Bob be sure to win for the following cases?
a.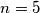
b.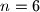
c.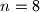
Justify your answer(s).
[For example, when n=4, Alice may choose the numbers 1, 5, 7, 9, which have the same pairwise sums as the numbers 2, 4, 6, 10, and hence Bob cannot be sure to win.]
 be a positive integer. Two players, Alice and Bob, are playing the following game:
be a positive integer. Two players, Alice and Bob, are playing the following game:- Alice chooses n real numbers; not necessarily distinct.
- Alice writes all pairwise sums on a sheet of paper and gives it to Bob. (There are
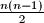 such sums; not necessarily distinct.)
such sums; not necessarily distinct.)- Bob wins if he finds correctly the initial n numbers chosen by Alice with only one guess.
Can Bob be sure to win for the following cases?
a.
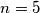
b.
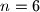
c.
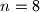
Justify your answer(s).
[For example, when n=4, Alice may choose the numbers 1, 5, 7, 9, which have the same pairwise sums as the numbers 2, 4, 6, 10, and hence Bob cannot be sure to win.]
 Školjka
Školjka 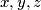 and
and  such that
such that 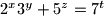
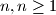 ,such that
,such that 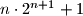 is a perfect square
is a perfect square 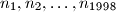 be positive integers such that
be positive integers such that 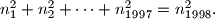 Show that at least two of the numbers are even.
Show that at least two of the numbers are even. 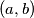 of positive integers for which the numbers
of positive integers for which the numbers 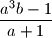 and
and 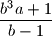 are both positive integers.
are both positive integers.  be an acute-angled triangle with
be an acute-angled triangle with 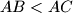 and let
and let  be the centre of its circumcircle
be the centre of its circumcircle  . Let
. Let  be a point on the line segment
be a point on the line segment  such that
such that 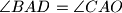 . Let
. Let  be the second point of intersection of
be the second point of intersection of  . If
. If 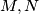 and
and  are the midpoints of the line segments
are the midpoints of the line segments 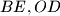 and
and  , respectively, show that the points
, respectively, show that the points 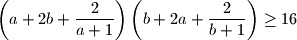
 and
and  such that
such that 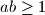 .
. 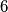 ?
?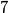 ?
? 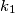 and
and 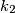 intersect at two points
intersect at two points  and
and  , and let t be a common tangent of
, and let t be a common tangent of  and
and  respectively. If
respectively. If 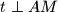 and
and 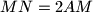 , evaluate the angle
, evaluate the angle 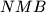 .
.  be positive real numbers such that
be positive real numbers such that 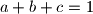 . Prove that
. Prove that 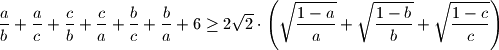 When does equality hold?
When does equality hold? 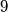 points inside a square of side length
points inside a square of side length  we can always find
we can always find  that form a triangle with area less than
that form a triangle with area less than 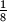 .
. 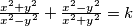 . Compute the following expression in terms of
. Compute the following expression in terms of  :
: 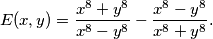
 be the incenter. Let
be the incenter. Let  and
and  respectively. The lines
respectively. The lines 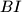 and
and 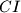 meet
meet  at
at  and
and  respectively. Prove that
respectively. Prove that 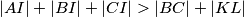 .
.  for which
for which 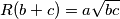 .
. 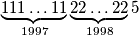 (which has 1997 of
(which has 1997 of  -s) is a perfect square.
-s) is a perfect square. 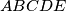 be a convex pentagon such that
be a convex pentagon such that 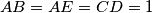 ,
, 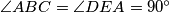 and
and 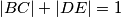 . Compute the area of the pentagon.
. Compute the area of the pentagon. 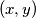 such that
such that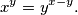
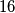 three digit numbers, using only three different digits in all, so that the all numbers give different residues when divided by
three digit numbers, using only three different digits in all, so that the all numbers give different residues when divided by 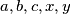 be five real numbers such that
be five real numbers such that 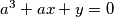 ,
, 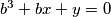 and
and 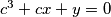 . If
. If 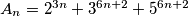 . Find the greatest common divisor of the numbers
. Find the greatest common divisor of the numbers 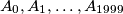 .
.  be a square with the side length 20 and let
be a square with the side length 20 and let 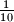 .
.  and
and  be positive reals such that
be positive reals such that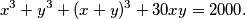 Show that
Show that 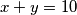 .
. 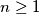 such that
such that 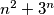 is the square of an integer.
is the square of an integer. 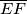 is placed on the side
is placed on the side 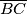 of a triangle
of a triangle 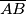 and
and 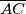 in the points
in the points  and
and 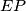 and
and 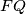 lies on the altitude from
lies on the altitude from  boys and
boys and  times as many matches as the girls. It is known that there were no draws. Find
times as many matches as the girls. It is known that there were no draws. Find 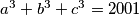 in positive integers.
in positive integers. 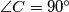 and
and 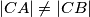 . Let
. Let 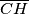 be an altitude and
be an altitude and 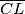 be an interior angle bisector. Show that for
be an interior angle bisector. Show that for 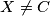 on the line
on the line 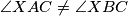 . Also show that for
. Also show that for 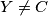 on the line
on the line 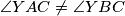 .
. 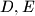 on the sides
on the sides 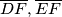 (with
(with 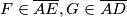 ) are the interior angle bisectors of the angles of the triangle
) are the interior angle bisectors of the angles of the triangle 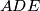 , prove that the sum of the areas of the triangles
, prove that the sum of the areas of the triangles 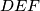 and
and 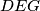 is at most equal with the area of the triangle
is at most equal with the area of the triangle 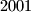 . Prove that we can find 3 vertices of
. Prove that we can find 3 vertices of 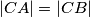 .
.  ).
). 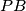 . Show that
. Show that 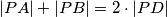 .
.