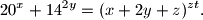We consider dissections of regular  -gons into
-gons into 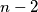 triangles by
triangles by 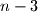 diagonals which do not intersect inside the
diagonals which do not intersect inside the  -gon. A bicoloured triangulation is such a dissection of an
-gon. A bicoloured triangulation is such a dissection of an  -gon in which each triangle is coloured black or white and any two triangles which share an edge have different colours. We call a positive interger
-gon in which each triangle is coloured black or white and any two triangles which share an edge have different colours. We call a positive interger 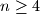 triangulable if every regular
triangulable if every regular  -gon has a bicoloured triangulation such that for each vertex
-gon has a bicoloured triangulation such that for each vertex  of the
of the  -gon the number of black triangles of which
-gon the number of black triangles of which  is a vertex is greater that the number of white triangles of which
is a vertex is greater that the number of white triangles of which  is a vertex.
is a vertex.
Find all triangulable numbers.
 -gons into
-gons into 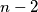 triangles by
triangles by 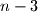 diagonals which do not intersect inside the
diagonals which do not intersect inside the  -gon. A bicoloured triangulation is such a dissection of an
-gon. A bicoloured triangulation is such a dissection of an  -gon in which each triangle is coloured black or white and any two triangles which share an edge have different colours. We call a positive interger
-gon in which each triangle is coloured black or white and any two triangles which share an edge have different colours. We call a positive interger 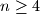 triangulable if every regular
triangulable if every regular  -gon has a bicoloured triangulation such that for each vertex
-gon has a bicoloured triangulation such that for each vertex  of the
of the  -gon the number of black triangles of which
-gon the number of black triangles of which  is a vertex is greater that the number of white triangles of which
is a vertex is greater that the number of white triangles of which  is a vertex.
is a vertex.Find all triangulable numbers.
For integers 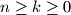 we define the bibinomial coefficient
we define the bibinomial coefficient 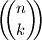 by
by 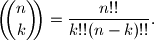 Determine all pairs
Determine all pairs 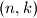 of integers with
of integers with 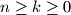 such that the corresponding bibinomial coefficient is an integer.
such that the corresponding bibinomial coefficient is an integer.
Remark. The double factorial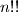 is defined to be the product of all even positive integers up to
is defined to be the product of all even positive integers up to  if
if  is even and the product of all odd positive integers up to
is even and the product of all odd positive integers up to  if
if  is odd. So e.g.
is odd. So e.g. 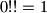 ,
, 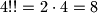 , and
, and 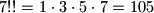 .
.
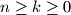 we define the bibinomial coefficient
we define the bibinomial coefficient 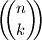 by
by 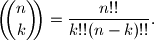 Determine all pairs
Determine all pairs 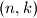 of integers with
of integers with 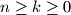 such that the corresponding bibinomial coefficient is an integer.
such that the corresponding bibinomial coefficient is an integer.Remark. The double factorial
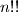 is defined to be the product of all even positive integers up to
is defined to be the product of all even positive integers up to  if
if  is even and the product of all odd positive integers up to
is even and the product of all odd positive integers up to  if
if  is odd. So e.g.
is odd. So e.g. 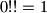 ,
, 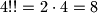 , and
, and 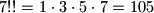 .
. Let  and
and  be positive integers. On a board consisting of
be positive integers. On a board consisting of 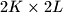 unit squares an ant starts in the lower left corner square and walks to the upper right corner square. In each step it goes horizontally or vertically to a neighbourning square. It never visits a square twice. At the end some squares may remain unvisited.
unit squares an ant starts in the lower left corner square and walks to the upper right corner square. In each step it goes horizontally or vertically to a neighbourning square. It never visits a square twice. At the end some squares may remain unvisited.
In some cases the collection of all unvisited squares forms a single rectangle. In such cases, we call this rectangle MEMOrable.
Determine the number of different MEMOrable rectangles.
Remark. Rectangles are different unless they consist of exactly the same squares.
 and
and  be positive integers. On a board consisting of
be positive integers. On a board consisting of 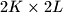 unit squares an ant starts in the lower left corner square and walks to the upper right corner square. In each step it goes horizontally or vertically to a neighbourning square. It never visits a square twice. At the end some squares may remain unvisited.
unit squares an ant starts in the lower left corner square and walks to the upper right corner square. In each step it goes horizontally or vertically to a neighbourning square. It never visits a square twice. At the end some squares may remain unvisited.In some cases the collection of all unvisited squares forms a single rectangle. In such cases, we call this rectangle MEMOrable.
Determine the number of different MEMOrable rectangles.
Remark. Rectangles are different unless they consist of exactly the same squares.
In Happy City there are 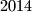 citizens called
citizens called 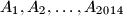 . Each of them is either happy or unhappy at any moment in time. The mood of any citizen
. Each of them is either happy or unhappy at any moment in time. The mood of any citizen  changes (from being unhappy to being happy or vice versa) if and only if some other happy citizen smiles at
changes (from being unhappy to being happy or vice versa) if and only if some other happy citizen smiles at  . On Monday morning there were
. On Monday morning there were  happy citizens in the city.
happy citizens in the city.
The following happened on Monday during the day: citizen smiled at citizen
smiled at citizen  , then
, then  smiled at
smiled at 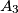 , etc., and, finally,
, etc., and, finally, 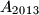 smiled at
smiled at 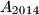 . Nobody smiled at anyone else apart from this. Exactly the same repeated on Tuesday, Wednesday and Thursday. There were exactly
. Nobody smiled at anyone else apart from this. Exactly the same repeated on Tuesday, Wednesday and Thursday. There were exactly 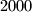 happy citizens on Thursday evening.
happy citizens on Thursday evening.
Determine the largest possible value of .
.
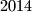 citizens called
citizens called 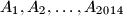 . Each of them is either happy or unhappy at any moment in time. The mood of any citizen
. Each of them is either happy or unhappy at any moment in time. The mood of any citizen  changes (from being unhappy to being happy or vice versa) if and only if some other happy citizen smiles at
changes (from being unhappy to being happy or vice versa) if and only if some other happy citizen smiles at  . On Monday morning there were
. On Monday morning there were  happy citizens in the city.
happy citizens in the city.The following happened on Monday during the day: citizen
 smiled at citizen
smiled at citizen  , then
, then  smiled at
smiled at 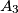 , etc., and, finally,
, etc., and, finally, 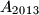 smiled at
smiled at 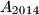 . Nobody smiled at anyone else apart from this. Exactly the same repeated on Tuesday, Wednesday and Thursday. There were exactly
. Nobody smiled at anyone else apart from this. Exactly the same repeated on Tuesday, Wednesday and Thursday. There were exactly 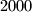 happy citizens on Thursday evening.
happy citizens on Thursday evening.Determine the largest possible value of
 .
. A finite set of positive integers  is called meanly if for each of its nonempty subsets the arithmetic mean of its elements is also a positive integer. In other words, A is meanly if
is called meanly if for each of its nonempty subsets the arithmetic mean of its elements is also a positive integer. In other words, A is meanly if 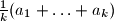 is an integer whenever
is an integer whenever 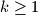 and
and 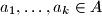 are distinct.
are distinct.
Given a positive integer , determine the least possible sum of the elements of a meanly
, determine the least possible sum of the elements of a meanly  -element set.
-element set.
 is called meanly if for each of its nonempty subsets the arithmetic mean of its elements is also a positive integer. In other words, A is meanly if
is called meanly if for each of its nonempty subsets the arithmetic mean of its elements is also a positive integer. In other words, A is meanly if 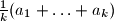 is an integer whenever
is an integer whenever 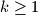 and
and 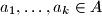 are distinct.
are distinct.Given a positive integer
 , determine the least possible sum of the elements of a meanly
, determine the least possible sum of the elements of a meanly  -element set.
-element set.  Školjka
Školjka 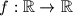 such that
such that 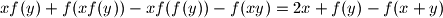 holds for all
holds for all 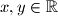 .
.  be a triangle with
be a triangle with 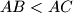 and incentre
and incentre  . Let
. Let  be the point on the side
be the point on the side  such that
such that  . Let
. Let  be the point on the line
be the point on the line 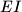 such that
such that 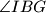 =
= 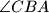 and such that
and such that 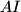 , the perpendicular to
, the perpendicular to 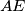 at
at 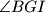 are concurrent.
are concurrent. 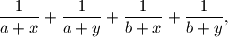 where
where  ,
,  ,
,  , and
, and  are positive real numbers satisfying the inequalities
are positive real numbers satisfying the inequalities 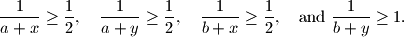
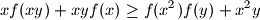 holds for all
holds for all  ,
,  , and
, and  in the points
in the points  ,
,  respectively. The angle bisector
respectively. The angle bisector  and
and  in the points
in the points  and
and  respectively. Let
respectively. Let  be the foot of the altitude through
be the foot of the altitude through 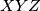 .
.  of the triangle
of the triangle  intersect
intersect 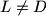 and denote the excentre of
and denote the excentre of  and
and 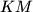 respectively.
respectively. ,
,  ,
, 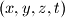 of positive integers such that
of positive integers such that