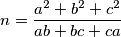The two figures depicted below, consisting of 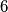 and
and  unit sqares respectively are called staircases.
unit sqares respectively are called staircases.
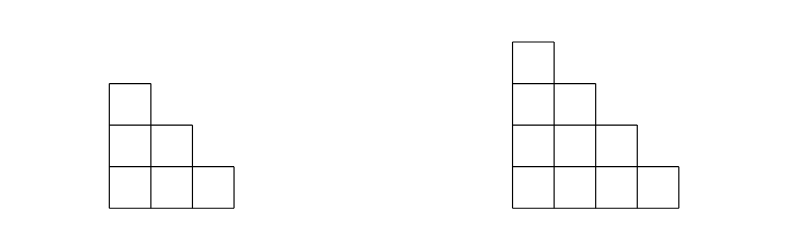
Consider a  board consisting of
board consisting of 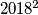 cells, each being an unit square. Two arbitrary cells were removed from the same row of the board. Prove that the rest of the board cannot be cut (along the cell borders) into staircases (possibly rotated).
cells, each being an unit square. Two arbitrary cells were removed from the same row of the board. Prove that the rest of the board cannot be cut (along the cell borders) into staircases (possibly rotated).
A group of pirates had an argument and now each of them holds some other two at gunpoint. All the pirates are called one by one in some order. If the called pirate is still alive, he shoots both pirates he is aiming at (some of whom might already be dead). All shots are immediately lethal. After all the pirates have been called, it turns out that exactly 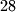 pirates have been killed.
pirates have been killed.
Prove that if the pirates have been called in whatever other order, at least  pirates would have been killed anyway.
pirates would have been killed anyway.
Let  be a positive integer and let
be a positive integer and let 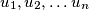 be positive integers not larger than
be positive integers not larger than 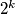 for some integer
for some integer 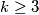 . A
. A 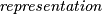 of a non-negative integer
of a non-negative integer  is a sequence of non-negative integers
is a sequence of non-negative integers 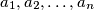 such that
such that 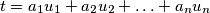 Prove that if a non-negative integer
Prove that if a non-negative integer  has a representation, then it also has a representation where less than
has a representation, then it also has a representation where less than 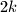 of the numbers
of the numbers 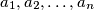 are non-zero.
are non-zero.
 Školjka
Školjka  denote the set of all positive rational numbers and let
denote the set of all positive rational numbers and let 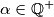 . Determine all functions
. Determine all functions 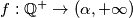 such that
such that 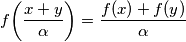 for all
for all 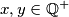
 be an acute-angled triangle with
be an acute-angled triangle with 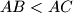 and let
and let  be the foot of its altitude from
be the foot of its altitude from  . Let
. Let  and
and  be the centroids of triangles
be the centroids of triangles 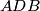 and
and 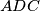 respectively. Let
respectively. Let  be a point on the line segment
be a point on the line segment 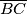 such that the points
such that the points 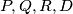 are concyclic.
are concyclic.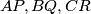 are concurrent.
are concurrent.  there exists an integer
there exists an integer 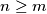 such that
such that 
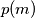 the smallest integer
the smallest integer 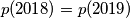 .
. 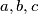 be positive real numbers such that
be positive real numbers such that 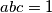 . Prove that
. Prove that 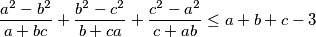
 with rational coefficients such that
with rational coefficients such that  polynomial with rational coefficients.
polynomial with rational coefficients. 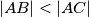 , and let
, and let 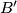 and
and 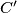 lie on the rays
lie on the rays  ,
,  respectively, so that points
respectively, so that points  ,
,  ,
,  . Prove that if
. Prove that if  is the midpoint of
is the midpoint of  is the orthocenter of
is the orthocenter of 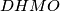 is a parallelogram.
is a parallelogram. 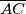 at
at  and the circumcircle of triangle
and the circumcircle of triangle 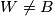 . Let
. Let  be the perpendicular projection of
be the perpendicular projection of 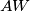 . The circumcircle of triangle
. The circumcircle of triangle 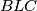 intersects line
intersects line 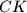 again at
again at 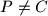 . Lines
. Lines 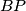 and
and  . Prove
. Prove 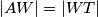 .
. 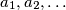 be a sequence of positive integers such that
be a sequence of positive integers such that 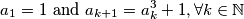 Prove that for every prime number
Prove that for every prime number  of the form
of the form 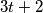 , where
, where  is divisible by
is divisible by