1. teža simulacija državnog natjecanja 2020.
Na kružnici je nasumično postavljeno  bijelih i
bijelih i  crnih kuglica. Počevši od proizvoljne bijele kuglice, u smjeru kazaljke na satu sve bijele kuglice su redom označene brojevima
crnih kuglica. Počevši od proizvoljne bijele kuglice, u smjeru kazaljke na satu sve bijele kuglice su redom označene brojevima 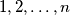 . Na isti način su i sve crne kuglice označene brojevima
. Na isti način su i sve crne kuglice označene brojevima 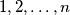 u smjeru suprotno od kazaljke na satu. Dokaži da postoji niz od
u smjeru suprotno od kazaljke na satu. Dokaži da postoji niz od  uzastopnih kuglica koje su označene brojevima
uzastopnih kuglica koje su označene brojevima 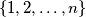 u nekom redoslijedu.
u nekom redoslijedu.
 Školjka
Školjka 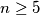 , brojevi
, brojevi 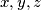 vrijedi
vrijedi 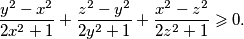
 i prirodne brojeve
i prirodne brojeve 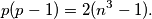
 i točka
i točka 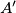 simetrična točki
simetrična točki  s obzirom na stranicu
s obzirom na stranicu  . Neka su
. Neka su  i
i  točke na stranicama
točke na stranicama  i
i  , redom, takve da je
, redom, takve da je 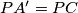 i
i 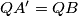 . Dokaži da okomica iz
. Dokaži da okomica iz  prolazi središtem opisane kružnice
prolazi središtem opisane kružnice