Općinsko natjecanje 1996 SŠ4 2
Dodao/la:
arhiva2. travnja 2012. Zadana su prva tri člana geometrijskog niza

,

,
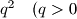
,
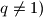
.

Odredite sve
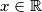
tako da kvadrati brojeva

,

,
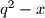
čine aritmetički niz, a zatim ispitajte predznak od

za razne vrijednosti
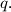

Izrazite razliku tog aritmetičkog niza kao funkciju od

. Koji uvjet zadovoljava

ako je ovaj niz rastući?
%V0
Zadana su prva tri člana geometrijskog niza $1$, $q$, $q^2 \quad (q > 0$, $q \neq 1)$.
$(a)$ Odredite sve $x \in \mathbb{R}$ tako da kvadrati brojeva $1-x$, $q-x$, $q^2-x$ čine aritmetički niz, a zatim ispitajte predznak od $x$ za razne vrijednosti $q.$
$(b)$ Izrazite razliku tog aritmetičkog niza kao funkciju od $q$. Koji uvjet zadovoljava $q$ ako je ovaj niz rastući?
Izvor: Općinsko natjecanje iz matematike 1996