Općinsko natjecanje 1997 SŠ4 2
Dodao/la:
arhiva2. travnja 2012. Nađite sve prirodne brojeve

za koje je
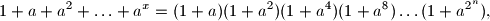
gdje je

realan i

prirodan broj.
%V0
Nađite sve prirodne brojeve $x$ za koje je $$
1 + a + a^2 + \ldots + a^x = (1 + a)(1 + a^2)(1
+ a^4)(1 + a^8)\ldots (1 + a^{2^n}),
$$ gdje je $a$ realan i $n$ prirodan broj.
Izvor: Općinsko natjecanje iz matematike 1997