Općinsko natjecanje 2005 SŠ4 3
Dodao/la:
arhiva2. travnja 2012. Zadan je rastav skupa prirodnih brojeva:
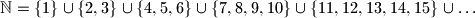
Ako je
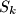
zbroj svih

brojeva u

-tom skupu iz gornjeg rastava, dokažite da vrijedi
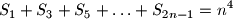
za svaki prirodni broj

.
%V0
Zadan je rastav skupa prirodnih brojeva: $$
\mathbb{N}= \{1\}\cup\{2,3\}\cup\{4,5,6\}\cup\{7,8,9,10\}
\cup\{11,12,13,14,15\}\cup\ldots
$$
Ako je $S_k$ zbroj svih $k$ brojeva u $k$-tom skupu iz gornjeg rastava, dokažite da vrijedi $$
S_1 + S_3 + S_5 + \ldots + S_{2n-1} = n^4
$$ za svaki prirodni broj $n$.
Izvor: Općinsko natjecanje iz matematike 2005