Općinsko natjecanje 2005 SŠ4 4
Dodao/la:
arhiva2. travnja 2012. Na krivulji s jednadžbom
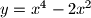
nalaze se

različite točke
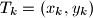
,
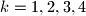
. Ako točke
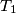
,
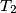
,
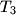
,
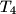
leže na jednom pravcu, dokažite da je
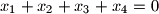
.
%V0
Na krivulji s jednadžbom $y=x^4-2x^2$ nalaze se $4$ različite točke $T_k=(x_k,y_k)$, $k=1,2,3,4$. Ako točke $T_1$, $T_2$, $T_3$, $T_4$ leže na jednom pravcu, dokažite da je $x_1+x_2+x_3+x_4=0$.
Izvor: Općinsko natjecanje iz matematike 2005