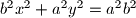
Zadana je elipsa s jednadžbom . Dokaži da sva sjecišta po dvije međusobno okomite tangente ove elipse leže na istoj kružnici.
%V0
Zadana je elipsa s jednadžbom $b^2 x^2 + a^2 y^2 = a^2 b^2$. Dokaži da sva sjecišta po dvije međusobno okomite tangente ove elipse leže na istoj kružnici.
Školjka 
. Dokaži da sva sjecišta po dvije međusobno okomite tangente ove elipse leže na istoj kružnici.