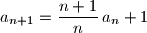
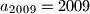
Zadan je niz realnih brojeva takav da je za svaki prirodan broj i . Odredi zbroj .
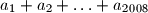
%V0
Zadan je niz realnih brojeva $a_n$ takav da je $a_{n+1}=\dfrac{n+1}{n}\,a_n + 1$ za svaki prirodan broj $n$ i $a_{2009}=2009$. Odredi zbroj $a_1+a_2+\ldots+a_{2008}$.
Školjka 
takav da je 
za svaki prirodan broj 
i 
. Odredi zbroj 
.