Državno natjecanje 1994 SŠ1 2
Kvaliteta:
Avg: 5,0Težina:
Avg: 2,5 Neka su  i
i  duljine osnovica trapeza. Dokažite:
duljine osnovica trapeza. Dokažite:
a) Duljina dužine paralelne s osnovicama, koja raspolavlja površinu trapeza, jednaka je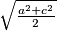 (kvadratna sredina).
(kvadratna sredina).
b) Duljina spojnice polovišta krakova jednaka je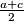 (aritmetička sredina).
(aritmetička sredina).
c) Duljina dužine paralelne osnovicama, koja dijeli trapez na dva međusobno slična trapeza, jednaka je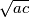 (geometrijska sredina).
(geometrijska sredina).
d) Duljina dužine paralelne s osnovicama kroz sjecište dijagonala, kojoj su krajevi na krakovima, jednaka je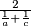 (harmonijska sredina).
(harmonijska sredina).
 i
i  duljine osnovica trapeza. Dokažite:
duljine osnovica trapeza. Dokažite:a) Duljina dužine paralelne s osnovicama, koja raspolavlja površinu trapeza, jednaka je
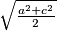 (kvadratna sredina).
(kvadratna sredina).b) Duljina spojnice polovišta krakova jednaka je
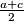 (aritmetička sredina).
(aritmetička sredina).c) Duljina dužine paralelne osnovicama, koja dijeli trapez na dva međusobno slična trapeza, jednaka je
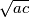 (geometrijska sredina).
(geometrijska sredina).d) Duljina dužine paralelne s osnovicama kroz sjecište dijagonala, kojoj su krajevi na krakovima, jednaka je
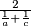 (harmonijska sredina).
(harmonijska sredina). Izvor: Državno natjecanje iz matematike 1994
 Školjka
Školjka 
