Nad stranicama trokuta

konstruirani su slični trokuti

,
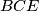
,
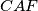
(
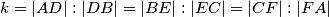
;
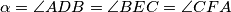
). Dokažite da su polovišta dužina

,

,

i
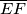
vrhovi paralelograma, čiji je jedan kut jednak

, a omjer duljina odgovarajućih stranica

.
%V0
Nad stranicama trokuta $ABC$ konstruirani su slični trokuti $ABD$, $BCE$, $CAF$ ($k = |AD|:|DB| = |BE|:|EC| = |CF|:|FA|$; $\alpha = \angle ADB = \angle BEC = \angle CFA$). Dokažite da su polovišta dužina $\overline{AC}$, $\overline{BC}$, $\overline{CD}$ i $\overline{EF}$ vrhovi paralelograma, čiji je jedan kut jednak $\alpha$, a omjer duljina odgovarajućih stranica $k$.