Školjka

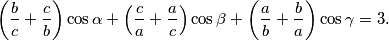
%V0 Dokažite da za svaki trokut sa stranicama $a$, $b$, $c$ i nasuprotnim kutovima $\alpha$, $\beta$, $\gamma$ vrijedi jednakost $$\left( \frac bc + \frac cb \right)\cos \alpha + \left( \frac ca + \frac ac \right)\cos \beta + \left( \frac ab + \frac ba \right)\cos \gamma = 3\text{.}$$