Državno natjecanje 2001 SŠ3 2
Dodao/la:
arhiva1. travnja 2012. Dan je trokut

takav da je
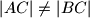
. Neka je

polovište stranice

,
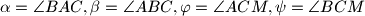
. Dokažite da je
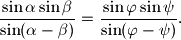
%V0
Dan je trokut $ABC$ takav da je $|AC| \neq |BC|$. Neka je $M$ polovište stranice $\overline{AB}$, $\alpha = \angle BAC, \beta = \angle ABC, \varphi = \angle ACM, \psi = \angle BCM$. Dokažite da je
$$\frac{\sin \alpha \sin \beta}{\sin(\alpha - \beta)} = \frac{\sin \varphi \sin \psi}{\sin (\varphi - \psi)}.$$
Izvor: Državno natjecanje iz matematike 2001