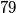
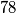
Dokažite da među svakih uzastopnih prirodnih brojeva postoji barem jedan čija je suma znamenaka djeljiva sa . Nađite niz od uzastopnih prirodnih brojeva sa svojstvom da suma znamenaka niti jednog od njih nije djeljiva sa .
%V0
Dokažite da među svakih $79$ uzastopnih prirodnih brojeva postoji barem jedan čija je suma znamenaka djeljiva sa $13$.
Nađite niz od $78$ uzastopnih prirodnih brojeva sa svojstvom da suma znamenaka niti jednog od njih nije djeljiva sa $13$.
Školjka 
uzastopnih prirodnih brojeva postoji barem jedan čija je suma znamenaka djeljiva sa 
.
uzastopnih prirodnih brojeva sa svojstvom da suma znamenaka niti jednog od njih nije djeljiva sa