Državno natjecanje 1999 SŠ3 1
Dodao/la:
arhiva1. travnja 2012. trokut

s koutovima

,

,

upisan je u pravokutnik
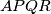
tako da tocka

lezi na stranici
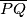
, a tocka

na stranici
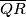
. dokazite da je
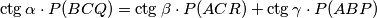
%V0
trokut $ABC$ s koutovima $\alpha$, $\beta$, $\gamma$ upisan je u pravokutnik $APQR$ tako da tocka $B$ lezi na stranici $\overline{PQ}$, a tocka $C$ na stranici $\overline{QR}$. dokazite da je
$\ctg\alpha\cdot P(BCQ) = \ctg\beta\cdot P(ACR) + \ctg\gamma\cdot P(ABP)
Izvor: Državno natjecanje iz matematike 1999