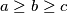
za duljine , i stranica trokuta vrijedi . vrhovi trokuta sredista su triju krugova s nenegativnim polumjerima. nikoja dva kruga nemaju zajednickih unutarnjih tocaka, niti obuhvacaju nikoji od preostala dva vrha trokuta. kolika je maksimalna povrsina koju prekrivaju ta tri kruga?
%V0
za duljine $a$, $b$ i $c$ stranica trokuta vrijedi $a \geq b \geq c$. vrhovi trokuta sredista su triju krugova s nenegativnim polumjerima. nikoja dva kruga nemaju zajednickih unutarnjih tocaka, niti obuhvacaju nikoji od preostala dva vrha trokuta. kolika je maksimalna povrsina koju prekrivaju ta tri kruga?
Školjka 
, 
i 
stranica trokuta vrijedi 
. vrhovi trokuta sredista su triju krugova s nenegativnim polumjerima. nikoja dva kruga nemaju zajednickih unutarnjih tocaka, niti obuhvacaju nikoji od preostala dva vrha trokuta. kolika je maksimalna povrsina koju prekrivaju ta tri kruga?