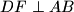
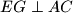
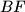
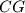
Dane su točke i , dok je varijabilna, takva da je fiksan. Polovišta stranica i su točke i redom. Točke i su takve da je i , a i su okomite na . Dokažite da umnožak ne ovisi o položaju točke .
%V0
Dane su točke $B$ i $C$, dok je $A$ varijabilna, takva da je $\angle BAC$ fiksan. Polovišta stranica $\overline{AB}$ i $\overline{AC}$ su točke $D$ i $E$ redom. Točke $F$ i $G$ su takve da je $DF \perp AB$ i $EG \perp AC$, a $BF$ i $CG$ su okomite na $BC$. Dokažite da umnožak $|BF| \cdot |CG|$ ne ovisi o položaju točke $A$.
Školjka 
i 
, dok je 
varijabilna, takva da je 
fiksan. Polovišta stranica 
i 
su točke 
i 
redom. Točke 
i 
su takve da je 
i 
, a 
i 
su okomite na 
. Dokažite da umnožak 
ne ovisi o položaju točke