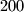
Skup sadrži prirodnih brojeva, od kojih je svaki manji od . Pokažite da postoji neprazan podskup od takav da je produkt brojeva iz potpuni kvadrat.
%V0
Skup $S$ sadrži $100$ prirodnih brojeva, od kojih je svaki manji od $200$. Pokažite da postoji neprazan podskup $T$ od $S$ takav da je produkt brojeva iz $T$ potpuni kvadrat.
Školjka 
sadrži 
prirodnih brojeva, od kojih je svaki manji od 
. Pokažite da postoji neprazan podskup 
od