Državno natjecanje 2005 SŠ3 2
Dodao/la:
arhiva1. travnja 2012. Upisana kružnica trokuta

dodiruje stranice

,

i

redom u točkama
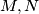
i

. Neka je

točka na manjem od dva luka

i

tangenta na taj luk s diralištem

. Tangenta

siječe
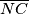
i
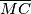
redom u točkama

i

. Dokažite da se pravci
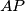
,
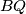
,
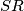
i

sijeku u jednoj točki.
%V0
Upisana kružnica trokuta $ABC$ dodiruje stranice $\overline{AC}$, $\overline{BC}$ i $\overline{AB}$ redom u točkama $M, N$ i $R$. Neka je $S$ točka na manjem od dva luka $MN$ i $t$ tangenta na taj luk s diralištem $S$. Tangenta $t$ siječe $\overline{NC}$ i $\overline{MC}$ redom u točkama $P$ i $Q$. Dokažite da se pravci $AP$, $BQ$, $SR$ i $MN$ sijeku u jednoj točki.
Izvor: Državno natjecanje iz matematike 2005