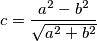
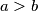
Duljine stranica trokuta su , i , . Dokaži da za kutove i , nasuprotne stranicama i , vrijedi .
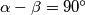
%V0
Duljine stranica trokuta su $a$, $b$ i $\displaystyle c = \frac{a^2 - b^2}{\sqrt{a^2 + b^2}}$, $a > b$. Dokaži da za kutove $\alpha$ i $\beta$, nasuprotne stranicama $a$ i $b$, vrijedi $\alpha-\beta = 90^{\circ}$.
Školjka 
, 
i 
, 
. Dokaži da za kutove 
i 
, nasuprotne stranicama 
.